A1.2 Data Representation
THEME A: SYSTEM FUNDAMENTALS
Data representation is fundamental to understanding how computers store and process information. This chapter covers number systems, character encoding, image representation, sound sampling, and data compression techniques.
Table of Contents
1.1 Number Systems
1.2 Text, Sound and Images
1.3 Data Storage and File Compression
1.1 Number Systems
Key Concepts
Computers use binary (base 2) to represent all data. Understanding how to convert between binary, denary (base 10), and hexadecimal (base 16) is essential for computer science.
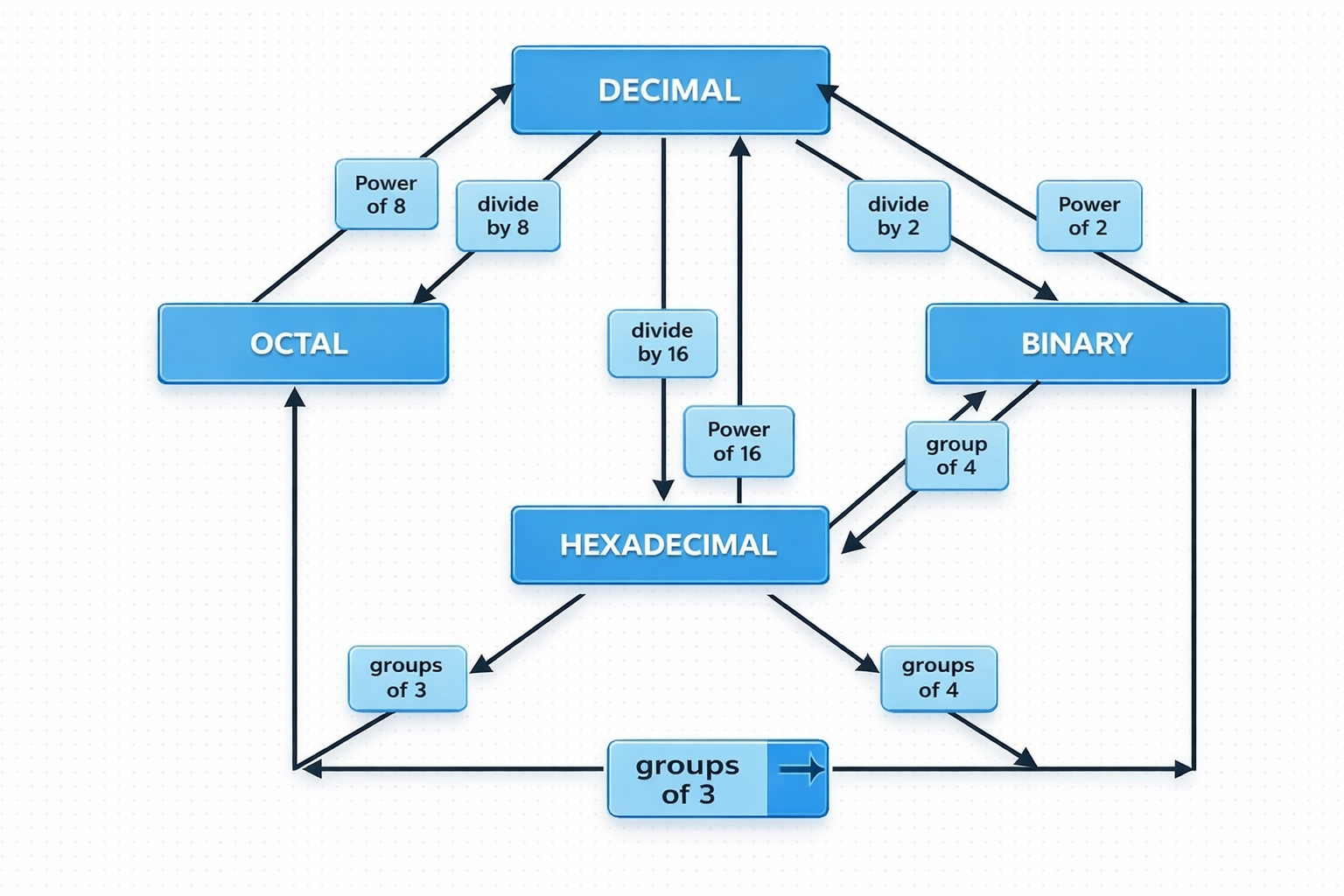
Understanding the Number System Diagram
Decimal as the Central Number System
The decimal number system (base 10) is placed at the center because it is the system humans use in daily life.
Converting from Decimal:
- •Decimal → Binary: Convert by repeatedly dividing by 2
- •Decimal → Octal: Convert by repeatedly dividing by 8
- •Decimal → Hexadecimal: Convert by repeatedly dividing by 16
Converting back to Decimal:
- •Binary uses powers of 2
- •Octal uses powers of 8
- •Hexadecimal uses powers of 16
Key Insight: This highlights that each number system is based on its base value.
Binary as the Foundation of Computing
The binary number system (base 2) is fundamental because computers operate using only 0s and 1s.
The diagram shows how binary connects easily to:
- •Octal (base 8) by grouping binary digits in groups of 3
- •Hexadecimal (base 16) by grouping binary digits in groups of 4
Why these groupings work:
Key Insight: This allows direct conversion between binary and hexadecimal without using decimal.
Purpose of Octal and Hexadecimal
Octal and Hexadecimal are included to show how large binary numbers can be written in a shorter and more readable form.
- •Octal compresses binary into groups of 3 bits
- •Hexadecimal compresses binary into groups of 4 bits
Real-World Application: Hexadecimal is especially important in memory addressing, machine code, and low-level programming.
Number System Comparison Table (0-15)
| Decimal | Hexadecimal | Binary (4-bit) |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
Note: Notice how each hexadecimal digit (0-F) corresponds exactly to a 4-bit binary pattern. This makes conversion between binary and hexadecimal straightforward by grouping binary digits in sets of 4.
Binary (Base 2)
Binary uses only two digits: 0 and 1. Each position represents a power of 2.
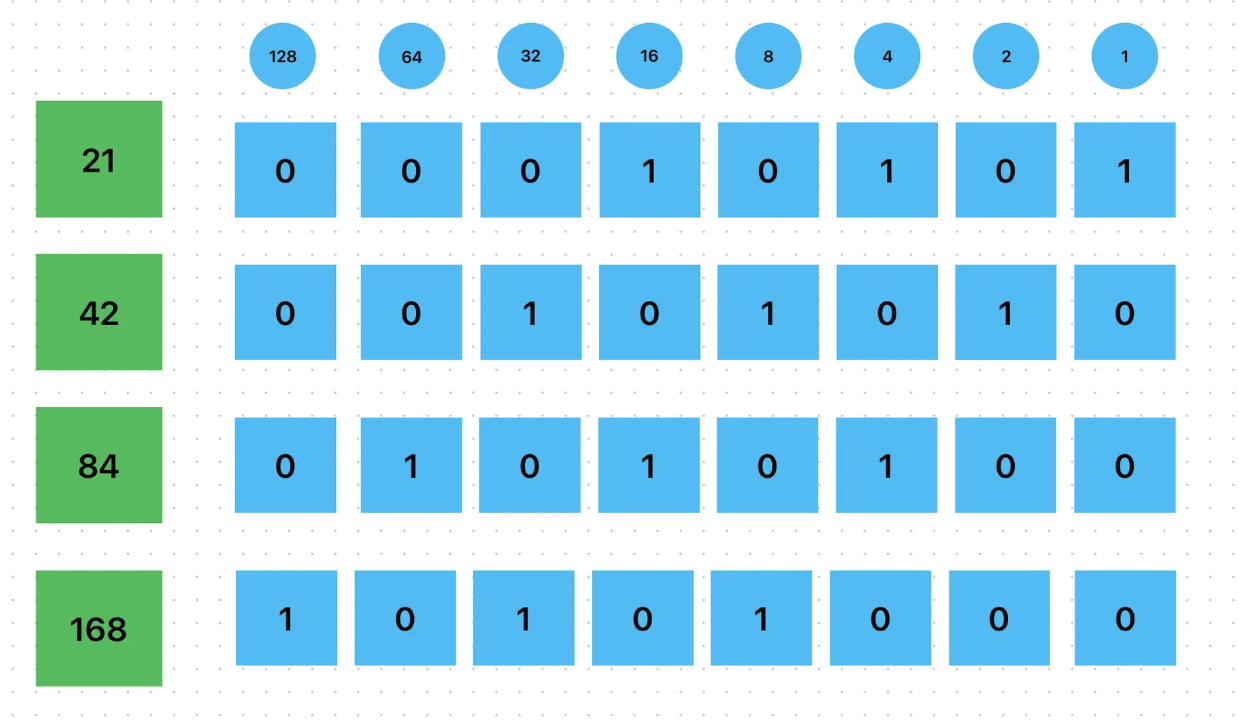
Binary to Denary Conversion
To convert binary to denary, multiply each digit by its position value (power of 2) and sum:
1 × 2³ = 1 × 8 = 8 0 × 2² = 0 × 4 = 0 1 × 2¹ = 1 × 2 = 2 1 × 2⁰ = 1 × 1 = 1
Denary to Binary Conversion
Repeatedly divide by 2 and collect remainders:
25 ÷ 2 = 12 remainder 1 12 ÷ 2 = 6 remainder 0 6 ÷ 2 = 3 remainder 0 3 ÷ 2 = 1 remainder 1 1 ÷ 2 = 0 remainder 1
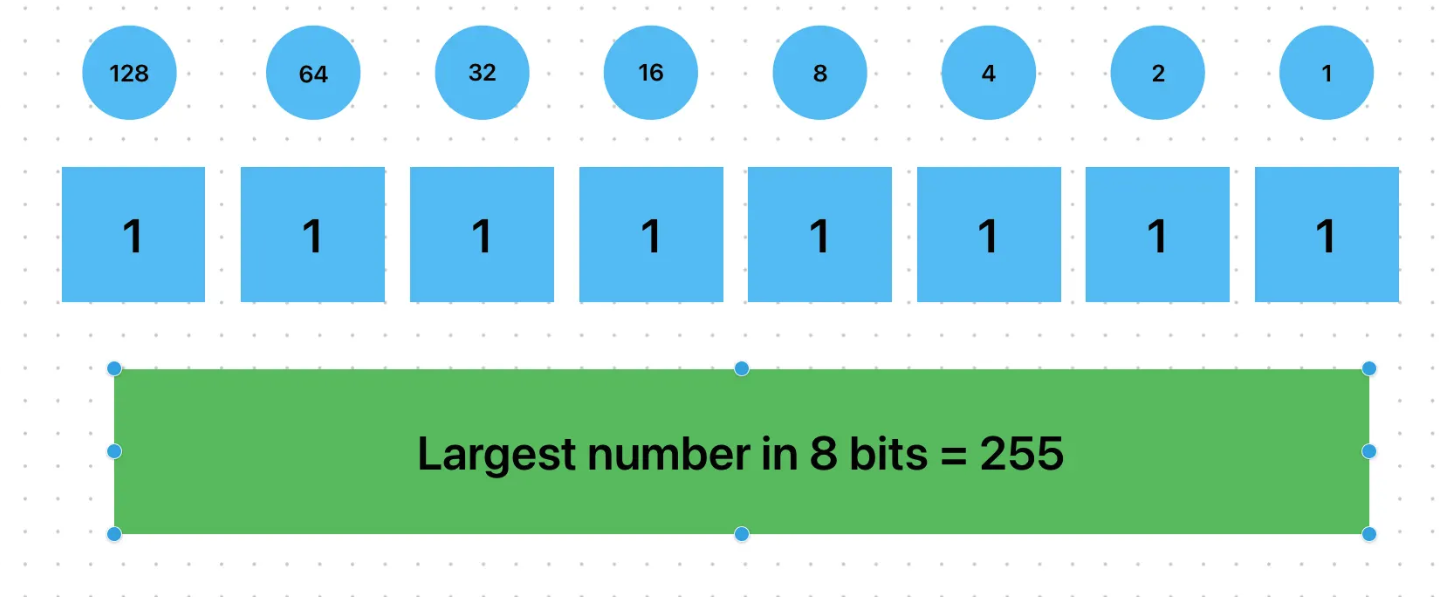
8-bit Binary Range
111111112)000000002)Practice Question
Past PaperThe hockey club wants to increase the number of people that can watch each match to 2000. The 8-bit binary register may no longer be able to store the value.
Give the smallest number of bits that can be used to store the denary value 2000.
Answer:
11 bits
Explanation: To find the smallest number of bits needed, we calculate 2n ≥ 2000. 210 = 1024 (too small), 211 = 2048 (can store values up to 2047, which includes 2000). Therefore, 11 bits is the minimum needed.
Uses of Binary
Why do computer systems use binary to represent data?
Computers use electronic circuits/Logic Gates that recognize only two voltage levels:
- •High voltage (1) → ON state
- •Low voltage (0) → OFF state
Two examples of how computer systems use binary to store different forms of data:
- Images – Stored using binary pixel values, where each pixel color is represented in binary (e.g., 8-bit color, 24-bit RGB).
- Audio Files – Sound waves are converted into binary samples using digital sampling techniques (e.g., MP3 files).
Hexadecimal (Base 16)
Hexadecimal uses 16 digits: 0-9 and A-F (where A=10, B=11, C=12, D=13, E=14, F=15). It's commonly used in computing because it's more compact than binary and easy to convert.
Hexadecimal to Denary
2 × 16¹ = 2 × 16 = 32 A × 16⁰ = 10 × 1 = 10
Binary to Hexadecimal
Group binary digits into groups of 4 (from right), then convert each group:
Tip: Hexadecimal is often prefixed with "0x" (e.g., 0x2A) or suffixed with "h" (e.g., 2Ah) in programming.
| Denary | Binary | Hexadecimal |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 10 | 1010 | A |
| 15 | 1111 | F |
| 16 | 10000 | 10 |
| 255 | 11111111 | FF |
Additional Conversion Examples
Example: Convert 45 (Decimal) to Binary
45 ÷ 2 = 22 remainder 1 22 ÷ 2 = 11 remainder 0 11 ÷ 2 = 5 remainder 1 5 ÷ 2 = 2 remainder 1 2 ÷ 2 = 1 remainder 0 1 ÷ 2 = 0 remainder 1
Example: Convert 101101 (Binary) to Decimal
1×2⁵ + 0×2⁴ + 1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 32 + 0 + 8 + 4 + 0 + 1
Example: Convert 2F (Hex) to Decimal
2 × 16¹ + F (15) × 16⁰ = 2 × 16 + 15 × 1 = 32 + 15
Uses of the Hexadecimal System
- ✓One hex digit represents 4 binary digits
- ✓Easier for humans to read, copy, and work with
1. Error Codes (Hex)
Used for debugging programs & memory addressing.
Example: Windows error code 0xC0000005
2. MAC Addresses (Hex)
Identifies devices uniquely on a network.
Example: 00-1C-B3-4F-25-FE
3. IP Addresses (Hex)
IPv4: 192.168.1.1 or C0.A8.01.01 (Hex)
IPv6: a8fb:7a88:fff0:0fff:3d21:2085:66fb:f0fa
4. HTML Color Codes
Used in web development for defining colors.
📝 Exam Keywords
Why a programmer may use hexadecimal to represent binary numbers:
- • Easier/quicker to understand/read/write
- • Easier/quicker to debug
- • Shorter representation (takes up less screen space)
Binary Operations
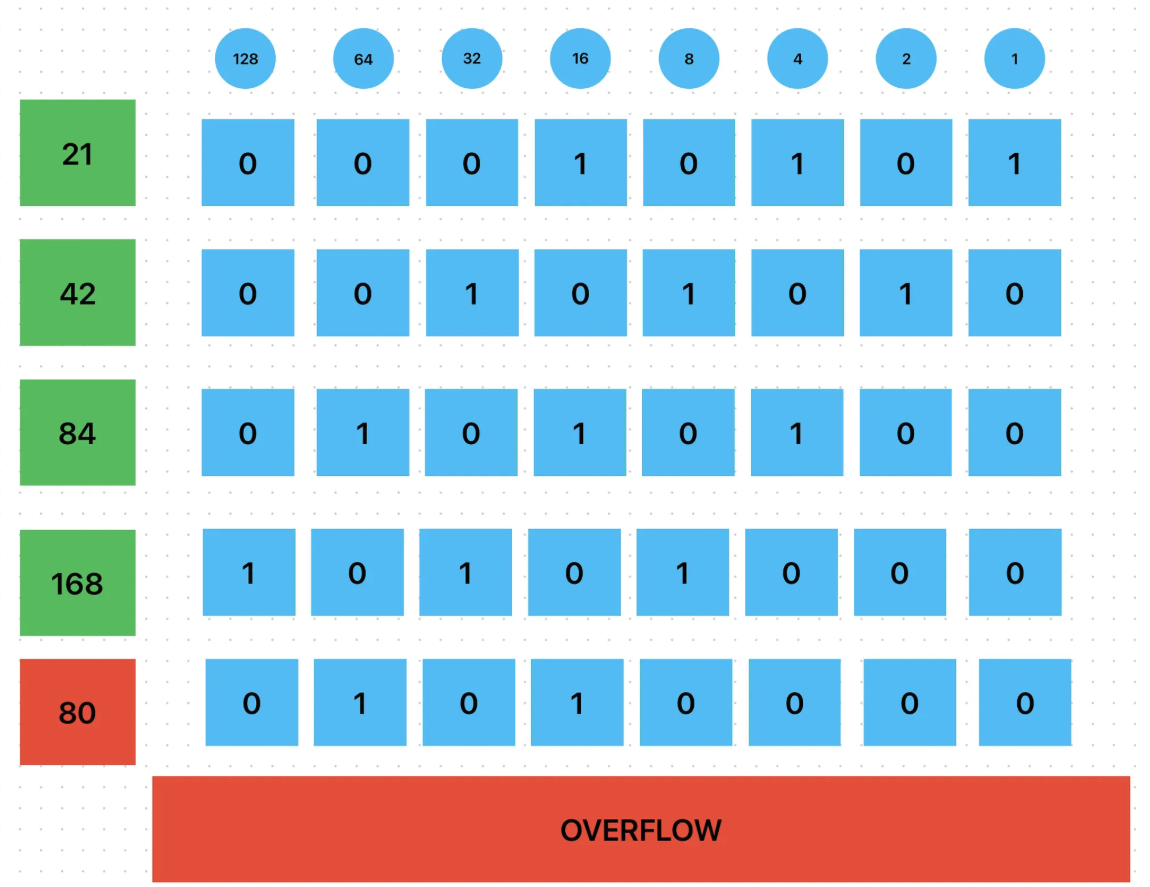
Binary Addition (8-bit)
Normal Example:
Overflow Example:
Overflow happens when the sum exceeds 8 bits!
Binary Shifting (8-bit)
Example of Left Shift (×2) and Right Shift (÷2):
Left shift multiplies, right shift divides. Overflow can occur in left shift.
This diagram shows how left shift and right shift operations work in binary. A left shift multiplies the number by 2 for each shift, while a right shift divides the number by 2, ignoring any remainder.
When a number is shifted left and the result exceeds the fixed bit limit (8 bits), the extra bit is lost, causing an overflow. As a result, the stored value becomes incorrect even though the operation is valid.
Negative Binary Representation (Two's Complement)
To represent negative numbers in binary, use two's complement:
- Write the positive number in binary
- Invert the bits (flip 0 to 1, 1 to 0)
- Add 1 to the result
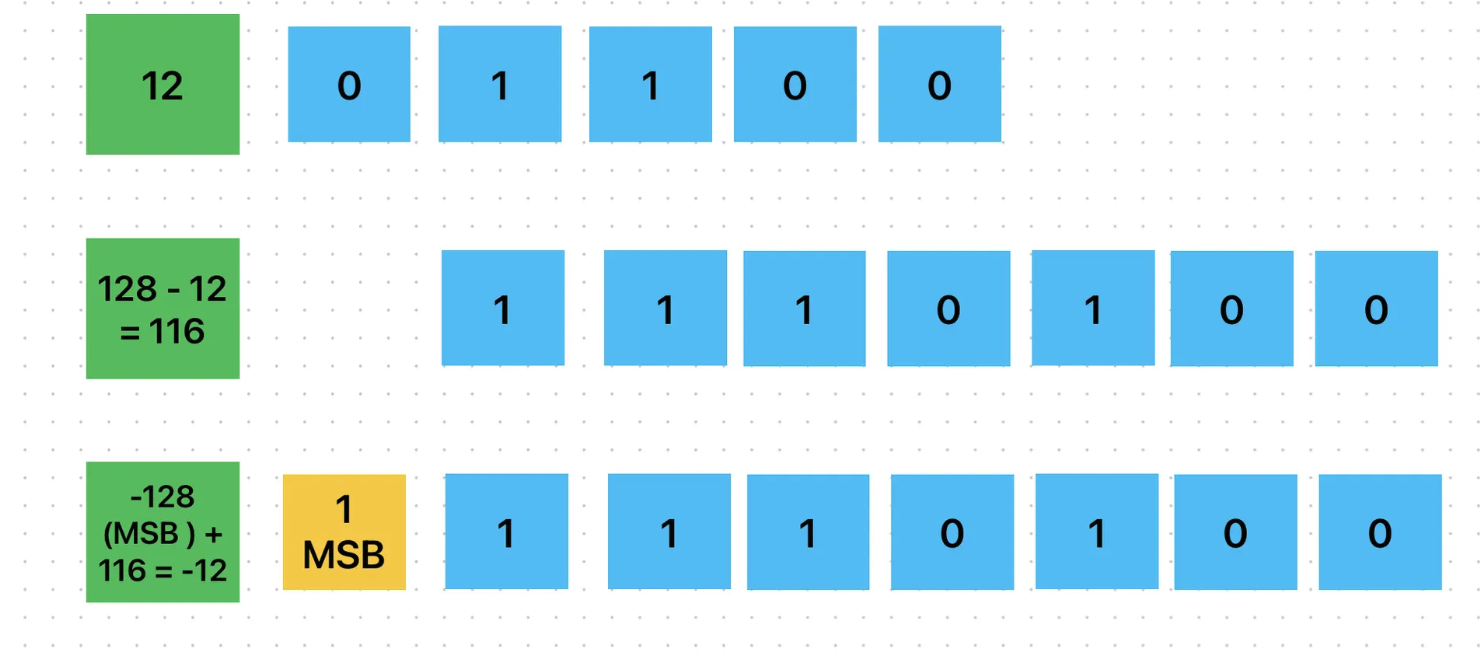
This diagram explains how two's complement is used to represent negative numbers in binary. To represent −12, we first write +12 in binary, then subtract it from 128 (for an 8-bit system) to get 116. Finally, the most significant bit (MSB) is set to 1, which represents −128. Adding −128 and 116 gives −12, showing how negative values are stored using two's complement.
Example: Convert -13 to 8-bit two's complement:
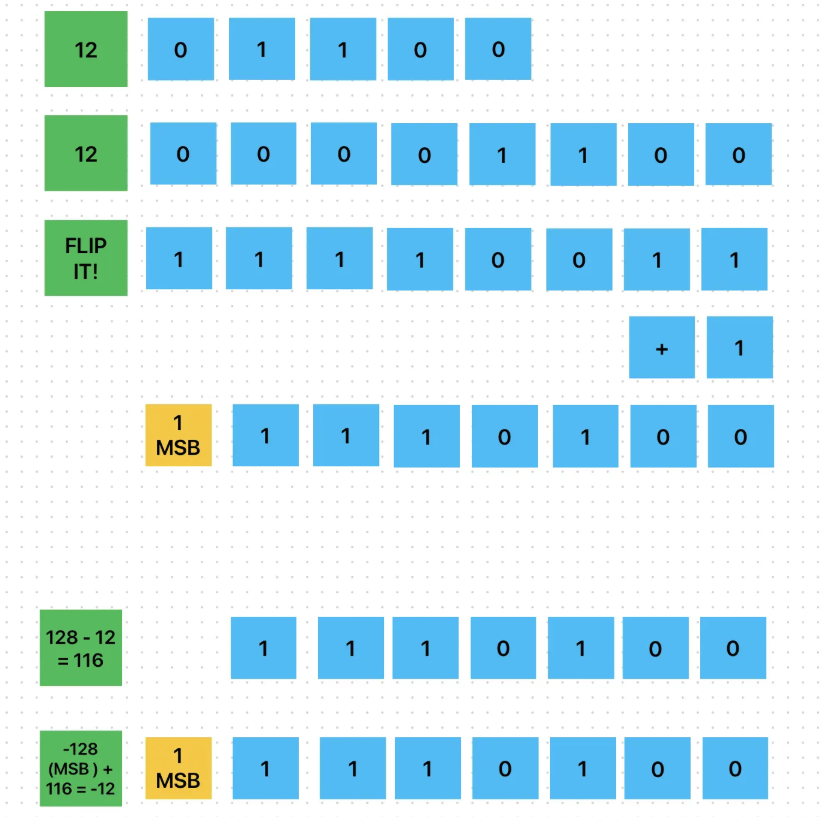
This diagram shows the second method of finding two's complement using the flip-and-add approach. First, the positive number (12) is written in 8-bit binary. All bits are then flipped (0 → 1, 1 → 0) to form the one's complement. Next, 1 is added to obtain the two's complement representation. The MSB becomes 1, indicating a negative number. This final binary value correctly represents −12.
📝 Exam Tip: This flip-and-add method is the most commonly used method in exams and real computer systems. Make sure you master this approach!
1.2 Text, Sound and Images
Character Sets
How Text is Stored in a Computer
1. Computers Understand Only Binary
A computer can only process binary digits (0s and 1s). All information, including text, numbers, and symbols, is ultimately represented in binary form.
2. Character Encoding Systems
Text is stored using a character encoding system such as ASCII or Unicode. Each character (letter, number, symbol) is assigned a unique numeric code, which is then stored as a binary value inside the computer.
3. Example: ASCII Encoding
4. Process of Storing Text
- Each character is converted into its numeric code
- The numeric code is then converted into binary digits
- The computer stores the binary values in memory
- When displayed, the binary values are mapped back to their corresponding characters
A character set is a system that computers use to store and represent text in binary format/denary. Each character (letter, number, or symbol) is assigned a unique binary code/Denary Number.
ASCII (American Standard Code for Information Interchange)
ASCII is a character encoding system that assigns a unique Denary/binary code to each character, allowing computers to represent text using 7-bit or 8-bit codes.
- •Introduced in 1963, updated in 1986
- •Uses 7-bit codes (128 characters: 0-127 in decimal, 00-7F in hexadecimal)
- •Includes English letters, numbers, symbols, and control codes
- •Examples: Lowercase 'a' = 97, Uppercase 'A' = 65
Process of Storing Text
- Each character is converted into its numeric code.
- The numeric code is then converted into binary digits.
- The computer stores the binary values in memory.
- When displayed, the binary values are mapped back to their corresponding characters.
✅ So, text in a computer is nothing but a sequence of binary codes representing characters.
Extended ASCII (8-bit)
- • Uses 8 bits (256 characters: 0-255 in decimal, 00-FF in hex)
- • Supports non-English alphabets and graphic symbols
- • Limitation: ASCII does not support non-Western languages (e.g., Chinese, Arabic, Hindi)
ASCII Character Table (Standard 7-bit ASCII: 0-127)
| Dec | Hex | Char | Dec | Hex | Char | Dec | Hex | Char | Dec | Hex | Char |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 00 | NUL | 7 | 07 | BEL | 8 | 08 | BS | 9 | 09 | TAB |
| 10 | 0A | LF | 13 | 0D | CR | 27 | 1B | ESC | 32 | 20 | SP |
| 48 | 30 | 0 | 49 | 31 | 1 | 50 | 32 | 2 | 51 | 33 | 3 |
| 52 | 34 | 4 | 53 | 35 | 5 | 54 | 36 | 6 | 55 | 37 | 7 |
| 56 | 38 | 8 | 57 | 39 | 9 | ||||||
| 65 | 41 | A | 66 | 42 | B | 67 | 43 | C | 68 | 44 | D |
| 69 | 45 | E | 70 | 46 | F | 71 | 47 | G | 72 | 48 | H |
| 73 | 49 | I | 74 | 4A | J | 75 | 4B | K | 76 | 4C | L |
| 77 | 4D | M | 78 | 4E | N | 79 | 4F | O | 80 | 50 | P |
| 81 | 51 | Q | 82 | 52 | R | 83 | 53 | S | 84 | 54 | T |
| 85 | 55 | U | 86 | 56 | V | 87 | 57 | W | 88 | 58 | X |
| 89 | 59 | Y | 90 | 5A | Z | ||||||
| 97 | 61 | a | 98 | 62 | b | 99 | 63 | c | 100 | 64 | d |
| 101 | 65 | e | 102 | 66 | f | 103 | 67 | g | 104 | 68 | h |
| 105 | 69 | i | 106 | 6A | j | 107 | 6B | k | 108 | 6C | l |
| 109 | 6D | m | 110 | 6E | n | 111 | 6F | o | 112 | 70 | p |
| 113 | 71 | q | 114 | 72 | r | 115 | 73 | s | 116 | 74 | t |
| 117 | 75 | u | 118 | 76 | v | 119 | 77 | w | 120 | 78 | x |
| 121 | 79 | y | 122 | 7A | z | ||||||
| 33 | 21 | ! | 34 | 22 | " | 35 | 23 | # | 36 | 24 | $ |
| 37 | 25 | % | 38 | 26 | & | 39 | 27 | ' | 40 | 28 | ( |
| 41 | 29 | ) | 42 | 2A | * | 43 | 2B | + | 44 | 2C | , |
| 45 | 2D | - | 46 | 2E | . | 47 | 2F | / | 58 | 3A | : |
| 59 | 3B | ; | 60 | 3C | < | 61 | 3D | = | 62 | 3E | > |
| 63 | 3F | ? | 64 | 40 | @ | 91 | 5B | [ | 92 | 5C | \ |
| 93 | 5D | ] | 94 | 5E | ^ | 95 | 5F | _ | 96 | 60 | ` |
| 123 | 7B | { | 124 | 7C | | | 125 | 7D | } | 126 | 7E | ~ |
| 127 | 7F | DEL |
Note: This table shows the most commonly used ASCII characters. Standard ASCII uses 7 bits (0-127), while Extended ASCII uses 8 bits (0-255). The table displays key characters including control codes, digits, uppercase and lowercase letters, and common symbols.
Unicode – A Universal Character Set
Developed in 1991 to overcome ASCII limitations. Can store all languages and symbols worldwide. Uses 16-bit or 32-bit codes instead of 7-bit ASCII.
Unicode Goals:
- ✓ Universal standard for all writing systems
- ✓ More efficient than ASCII
- ✓ Fixed encoding (16-bit or 32-bit per character)
- ✓ Supports private use characters (for unique languages like Chinese, Japanese)
Unicode Character Table (Examples from Different Languages)
| Decimal | Hexadecimal | Binary (16-bit) | Character | Language/Script | Description |
|---|---|---|---|---|---|
| 65 | 0041 | 0000000001000001 | A | English (Latin) | Uppercase A |
| 97 | 0061 | 0000000001100001 | a | English (Latin) | Lowercase a |
| 20013 | 4E2D | 0100111000101101 | 中 | Chinese (Simplified) | Middle/Center |
| 25991 | 6587 | 0110010110000111 | 文 | Chinese (Simplified) | Text/Writing |
| 22269 | 56FD | 0101011011111101 | 国 | Chinese (Simplified) | Country |
| 1575 | 0627 | 0000011000100111 | ا | Arabic | Alif |
| 1576 | 0628 | 0000011000101000 | ب | Arabic | Ba |
| 1587 | 0633 | 0000011000110011 | س | Arabic | Seen |
| 2325 | 0915 | 0000100100010101 | क | Hindi (Devanagari) | Ka |
| 2366 | 093E | 0000100100111110 | ा | Hindi (Devanagari) | Vowel sign |
| 2360 | 0938 | 0000100100111000 | श | Hindi (Devanagari) | Sha |
| 12354 | 3042 | 0011000001000010 | あ | Japanese (Hiragana) | A |
| 12356 | 3044 | 0011000001000100 | い | Japanese (Hiragana) | I |
| 12358 | 3046 | 0011000001000110 | う | Japanese (Hiragana) | U |
| 8730 | 221A | 0010001000011010 | √ | Mathematical | Square root |
| 8712 | 2208 | 0010001000001000 | ∈ | Mathematical | Element of |
| 8747 | 222B | 0010001000101011 | ∫ | Mathematical | Integral |
| 960 | 03C0 | 0000001111000000 | π | Mathematical | Pi |
| 8364 | 20AC | 0010000010101100 | € | Currency | Euro |
| 8377 | 20B9 | 0010000010111001 | ₹ | Currency | Indian Rupee |
| 165 | 00A5 | 0000000010100101 | ¥ | Currency | Yen/Yuan |
| 163 | 00A3 | 0000000010100011 | £ | Currency | Pound Sterling |
| 128512 | 1F600 | 11111011000000000 | 😀 | Emoji | Grinning face |
| 128525 | 1F60D | 11111011000001101 | 😍 | Emoji | Heart eyes |
| 128151 | 1F497 | 11111010010010111 | 💗 | Emoji | Growing heart |
| 127925 | 1F3B5 | 11111001110110101 | 🎵 | Emoji | Musical note |
Note: Unicode can represent over 1.1 million characters from hundreds of writing systems worldwide. The table above shows examples from different languages and scripts to demonstrate Unicode's universality. Unicode uses 16-bit (UTF-16) or 32-bit (UTF-32) encoding, allowing it to support characters from English, Chinese, Arabic, Hindi, Japanese, and many other languages, as well as mathematical symbols, currency symbols, and emojis.
Unicode supports:
English, French, Chinese, Hindi, Arabic, and more! Mathematical symbols, emojis (😂, ❤️, 🎵), and currency symbols (€, ₹, $).
ASCII vs Unicode Comparison
| Feature | ASCII | Unicode |
|---|---|---|
| Year | 1963 | 1991 |
| Bit Length | 7-bit (128 chars) or 8-bit (256 chars) | 16-bit or 32-bit (65,536+ chars) |
| Languages | English only | All languages |
| Symbols & Emojis | No | Yes ✓ |
| Control Characters | Yes ✓ | Yes ✓ |
| Storage Efficiency | Small file sizes | Larger file sizes |
Note: ASCII is a subset of Unicode. Unicode keeps the first 128 ASCII characters the same to maintain compatibility. Unicode is the modern standard used in web development, databases, and programming.
Explain how the word 'RED' is represented using a character set:
- • Unique binary/denary number given/stored for each character
- • The code for R is stored, then the code for E, then D in sequence
Image Representation
What is a Pixel?
A pixel (short for "picture element") is the smallest unit of a digital image or display. Can be Square/Circle.
What is a Bitmap Image?
A bitmap image is made up of small picture elements (pixels) arranged in a two-dimensional grid. Each pixel is represented using binary values.
Pixel Representation in Binary:
- ✓Black & White Image → 1 bit per pixel (0 = black, 1 = white)
- ✓2-bit Colour Depth → 4 colours (00, 01, 10, 11)
- ✓3-bit Colour Depth → 8 colours (000 to 111)
- ✓8-bit Colour Depth → 256 colours (2⁸ = 256)
- ✓24-bit Colour Depth → 16.7 million colours (2²⁴ = 16,777,216)
Colour Depth
Colour depth is the number of bits used per pixel to represent different colours.
Formula: Total Colours = 2ⁿ, where n = number of bits per pixel
| Colour Depth (bits per pixel) | Total Colours |
|---|---|
| 1-bit (Black & White) | 2 |
| 2-bit | 4 |
| 3-bit | 8 |
| 8-bit | 256 |
| 16-bit | 65,536 |
| 24-bit | 16.7 million |
| 32-bit | 4.3 billion |
Higher colour depth = Better image quality but larger file size.
Image Resolution & Quality
Resolution refers to the number of pixels in an image (width × height).
Higher resolution means more pixels, leading to better quality but larger file size.
| Resolution | Total Pixels |
|---|---|
| 1024 × 768 | 786,432 pixels |
| 1920 × 1080 | 2,073,600 pixels |
| 4K (3840 × 2160) | 8,294,400 pixels |
Higher resolution images require more storage.
Effect of Resolution on Image Quality
High Resolution
Sharp and detailed image ✓
Low Resolution
Pixelated and blurry image ✗
Example: A 4K image is much clearer than a 480p image due to more pixels. Lowering resolution reduces file size but decreases image quality.
Image Size Calculation:
Data Storage Units
Basic Units
- •Bit: The smallest unit of data in computing, representing a 0 or 1
- •Nibble: A 4-bit group (half of a byte)
- •Byte: A group of 8 bits
Memory Aid: "Ko Ma Gi To Pie"
Remember this acronym to help you recall the order of binary units: Ko Ma Gi To Pie
The order is very important when doing conversions!
Binary Units (KiB, MiB, GiB)
| Unit | Equivalent |
|---|---|
| 1 Bit | 0 or 1 |
| 1 Nibble | 4 Bits |
| 1 Byte | 8 Bits |
| 1 KiB | 1024 Bytes |
| 1 MiB | 1024 KiB |
| 1 GiB | 1024 MiB |
| 1 TiB | 1024 GiB |
| 1 PiB | 1024 TiB |
| 1 EiB | 1024 PiB |
Used by: Computer Memory (RAM)
Decimal Units (KB, MB, GB)
| Unit | Equivalent |
|---|---|
| 1 KB | 1,000 Bytes |
| 1 MB | 1,000 KB |
| 1 GB | 1,000 MB |
| 1 TB | 1,000 GB |
| 1 PB | 1,000 TB |
| 1 EB | 1,000 PB |
Used by: Hard Drive/SSD manufacturers
Note: Storage capacity is measured in both decimal (KB, MB) and binary (KiB, MiB) formats. Kilobyte (KB) = 1000 bytes (decimal), Kibibyte (KiB) = 1024 bytes (binary).
Quick Conversions:
Sound Representation
Key Terms
Sample Rate/Sampling Frequency
Number of audio samples taken per second when converting analog sound wave to digital format. It is measured in Hertz (Hz).
Sample Resolution (Bit Depth)
Number of bits used to represent each audio sample in digital sound recording. Determines accuracy and dynamic range of the recorded sound.
Why recording sound with a higher sampling resolution creates a more accurate recording:
- • More bits allocated to each amplitude
- • Amplitudes can be more precise
- • A wider range of amplitudes can be recorded
One other way to improve accuracy: Increase sample rate
How Sampling is Used to Record a Sound Clip
Sampling is the process of converting an analog sound wave into a digital format that can be stored and processed by a computer.
Steps:
- Sound Wave is captured → Microphone converts the analog sound wave into an electrical signal
- ADC (Analog to Digital Converter) → The continuous sound wave is measured at regular intervals (samples)
- Sampling Rate (Frequency) → The number of samples taken per second measured in Hertz (Hz)Example: 44.1 kHz means 44,100 samples per second (CD-Quality)
- Quantization → Each sample is assigned a numeric value (Bit Depth) representing the amplitude (loudness) of the sound at that moment
- Binary Storage → Sample value is stored as binary data allowing digital playback
Impact of Sampling Rates:
- • High Sampling Rate → More accurate sound reproduction but larger file size
- • Higher Bit Depth → More precise amplitude storage, leading to better sound quality
- • Lower Sampling Rate → Less accurate, e.g., muffled or robotic sound
Common Formats: MP3, WAV, AAC
Sampling
Sound is an analog signal (continuous wave). To store it digitally, we must sample the sound wave at regular intervals and convert each sample to a binary number.
Key Terms:
- Sample Rate:
- Number of samples taken per second (Hz). Common: 44.1 kHz, 48 kHz
- Bit Depth:
- Number of bits per sample. Common: 16-bit, 24-bit
- File Size Calculation:
- Size = Sample Rate × Bit Depth × Duration × Channels
Example Calculation:
Quality vs. File Size: Higher sample rates and bit depths produce better quality but larger files. Compression (MP3, AAC) reduces file size while maintaining acceptable quality.
1.3 Data Storage and File Compression
Metadata
What is Metadata?
Metadata is data about data. It provides information about a file's properties, characteristics, and attributes without being part of the actual content.
Think of metadata as a "label" or "tag" that describes what the file contains, when it was created, who created it, and other relevant information.
Examples of Metadata:
📷Image Metadata
Common image metadata includes:
- File name: photo.jpg
- File size: 2.5 MB
- Dimensions: 1920 × 1080 pixels
- Resolution: 72 DPI (dots per inch)
- Color depth: 24-bit (RGB)
- Date created: 2024-01-15 14:30:25
- Camera model: Canon EOS 5D
- Location (GPS): Latitude: 28.6139°N, Longitude: 77.2090°E
- Author/Photographer: John Doe
🎵Audio/Song Metadata
Common audio metadata (ID3 tags) includes:
- Title: "Bohemian Rhapsody"
- Artist: Queen
- Album: A Night at the Opera
- Genre: Rock
- Year: 1975
- Duration: 5:55 (5 minutes 55 seconds)
- Bit rate: 320 kbps
- Sample rate: 44.1 kHz
- File format: MP3
- File size: 13.6 MB
🎬Video Metadata
Common video metadata includes:
- Title: vacation_video.mp4
- Duration: 00:15:30 (15 minutes 30 seconds)
- Resolution: 1920 × 1080 (Full HD)
- Frame rate: 30 fps (frames per second)
- Video codec: H.264
- Audio codec: AAC
- File size: 450 MB
- Date recorded: 2024-07-20
- Camera/Device: iPhone 14 Pro
📄Document Metadata
Common document metadata includes:
- Title: "IGCSE Computer Science Notes"
- Author: Jane Smith
- Created date: 2024-01-10
- Modified date: 2024-01-25
- Number of pages: 45
- Word count: 12,500 words
- File format: PDF
- File size: 3.2 MB
- Subject/Tags: Education, Computer Science, IGCSE
Why is Metadata Important?
- ✓Organization: Helps organize and search for files easily
- ✓Identification: Provides information about file origin, creator, and purpose
- ✓Compatibility: Helps software understand how to process the file
- ✓Copyright: Can include copyright and licensing information
- ✓Search: Enables better search and filtering of files
Why is Data Compression Needed?
Files such as images, videos, and sound can be very large. Compression helps in:
📝 Exam Keywords
- ✓Saving storage space (reduces file size on hard drives and cloud storage)
- ✓Faster streaming (reduces buffering for music/videos)
- ✓Faster downloads/uploads (less time to transfer files)
- ✓Reduces network bandwidth usage (less internet data used)
- ✓Cost-saving (cloud storage and internet service providers charge based on data usage)
Key Point: Compressed files use fewer bits, leading to faster transmission and reduced storage costs.
Types of File Compression
| Compression Type | Definition | Key Features | Examples |
|---|---|---|---|
| Lossy Compression | Removes some data permanently | Smaller file size, cannot recover original | MP3, MP4, JPEG |
| Lossless Compression | Reduces file size without losing any data | Can fully restore original file | RLE, ZIP, PNG |
Compression Techniques
Lossless Compression
Original data can be perfectly reconstructed. No information is lost.
- •Run-Length Encoding (RLE): Replaces repeated sequences with count + value
- •Dictionary Encoding: Replaces common patterns with shorter codes
- •Examples: ZIP, PNG, FLAC
- •Use cases: Text files, program code, medical images
Past Paper Question: How does a lossless algorithm work?
Question: Explain how a lossless compression algorithm works.
Answer (Any three points):
- •The size of the file is reduced without permanently removing any data.
- •A compression algorithm is used, such as Run Length Encoding (RLE).
- •Repeating pixels are identified / Patterns are identified.
- •These patterns are stored with the number of times they are repeated.
- •The patterns are indexed for efficient storage and retrieval.
Lossy Compression
Some data is permanently removed. Original cannot be perfectly reconstructed, but file size is significantly reduced.
- •JPEG: Removes details imperceptible to human eye
- •MP3: Removes frequencies humans can't hear well
- •Examples: JPEG, MP3, MPEG video
- •Use cases: Photos, music, videos (where small quality loss is acceptable)
Lossy Compression Formats
MP3 (MPEG-3) - Lossy Compression for Audio
- ✓ Reduces audio file size by 90%
- ✓ Removes frequencies humans can't hear
- ✓ Uses Perceptual Music Shaping (keeps louder sounds, removes softer ones)
- ✓ Reduces Bit Depth
MP4 (MPEG-4) - Lossy Compression for Video
- ✓ Stores multimedia files (video, audio, images, animations)
- ✓ Smaller file size, retains acceptable quality
- ✓ Common for online streaming (Netflix, YouTube, etc.)
JPEG - Lossy Compression for Images
- ✓ Reduces Colour Depth
- ✓ Removes small colour details that the human eye doesn't notice
- ✓ Splits images into 8×8 pixel blocks to discard unnecessary data
- ✓ Reduces resolution
JPEG is widely used for online images, as the reduction in quality is often unnoticeable.
Lossless Compression - Run-Length Encoding (RLE)
A specialized algorithm that supports the compression of files by replacing repeated data with a symbol and a count. It's a lossless compression technique.
How RLE Works:
- ✓ Replaces repeated characters with a count + value
- ✓ Works best on long runs of repeating data
Limitation: Doesn't work well if no repeating characters are present (e.g., cdcdcdcdcd).
RLE Example 1: Simple Pattern (Black & White Only)
Color Encoding:
For black and white images, we use a simple format:
- 0 = Black
- 1 = White
Note: RGB format (Red, Green, Blue values) is only needed for color images. For black and white, we simply use 0 or 1.
8×8 Pixel Grid (Capital Letter F):
RLE Encoding Process:
Reading the grid row by row from left to right, we group consecutive pixels of the same color:
RLE Output (format: count, color) where 0 = black, 1 = white:
Note: For black and white images, we use a simple format (count, color) where 0 = black and 1 = white. RGB format is only needed for color images.
File Size Calculations:
Uncompressed File Size:
Compressed File Size (RLE):
Compression Ratio: 8 bytes ÷ 28 bytes = 1:3.5 (Actually increases size - RLE is less efficient for small, simple images)
Note: RLE works best for images with large areas of the same color. For this small 8×8 image, uncompressed format is actually smaller.
Conclusion:
Important Note about RLE for Small Images:
- For this small 8×8 image, RLE actually increases the file size (8 bytes → 28 bytes)
- This happens because storing the count and color values (2 bytes per run) takes more space than the simple 1-bit-per-pixel format
- RLE works best for larger images with long runs of the same color
- For very small images, the uncompressed format (1 bit per pixel) is more efficient
Key Takeaway: RLE compression is most effective when images have large areas of uniform color and when the image size is substantial enough that the overhead of storing run-lengths is offset by the compression benefits.
RLE Example 2: Complex Pattern (Black, White & Red)
Color Definitions (RGB Values):
| Color | Red | Green | Blue |
|---|---|---|---|
| Black | 0 | 0 | 0 |
| White | 255 | 255 | 255 |
| Red | 255 | 0 | 0 |
8×8 Pixel Grid (Pattern with Colors):
RLE Encoding Process:
Reading the grid row by row from left to right, we group consecutive pixels of the same color:
RLE Output (format: count, red, green, blue):
File Size Calculations:
Uncompressed File Size:
Compressed File Size (RLE):
Compression Ratio: 192 bytes ÷ 96 bytes = 2:1
Conclusion:
RLE still works for this image, but less efficiently because:
- The pattern has more color changes (black, white, and red)
- More runs are needed to represent the same 64 pixels (24 runs)
- The compression ratio is 2:1
- RLE works best when there are longer runs of the same color
Note: RLE would work poorly for complex images with many color changes (e.g., photographs), as there would be few repeating sequences to compress.
Describe how lossless compression compresses a text file:
- • A compression algorithm is used
- • Such as RLE/run length encoding
- • Repeating characters are identified / Patterns are identified
- • And indexed
- • With number of occurrences
- • With their position
Comparing Lossy vs. Lossless Compression
| Feature | Lossy Compression | Lossless Compression |
|---|---|---|
| File Size | Smaller | Larger |
| Data Loss | Yes (Irreversible) | No (Reversible) |
| Common Formats | MP3, MP4, JPEG | RLE, ZIP, PNG |
| Best for | Music, video, photos | Documents, software, images |
| Quality Loss? | Yes | No |
Choosing Compression: Need high quality? → Use Lossless RLE. Need smaller files? → Use Lossy (JPEG, MP3, MP4).
Compression Ratio
Compression ratio = Original size ÷ Compressed size
Important: Lossy compression is acceptable for media files but should never be used for text documents, program code, or any data where accuracy is critical.
Chapter Summary
- Number systems (Binary, Denary, Hexadecimal) are fundamental to computing
- Character encoding (ASCII, Unicode) allows text representation in binary
- Images are represented as grids of pixels with color depth determining quality
- Sound is digitized through sampling at regular intervals
- Compression reduces file sizes (lossless preserves data, lossy sacrifices some quality)
9. Logic Gates
Logic gates are the fundamental building blocks of all digital systems. They are electronic circuits that take binary inputs and produce a single binary output based on a logical rule.
Purpose (Real-World & Computer)
- Decision Making: "Unlock door IF (Pin is Correct AND Biometric Matches)".
- Arithmetic: Adding binary numbers in the CPU (ALU).
- Storage: Create flip-flops to store bits (RAM/Registers).
- Control: Traffic lights, elevators, safety alarms.
Basic Logic Gates
AND Gate
Output 1 only if BOTH inputs are 1.
| A | B | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR Gate
Output 1 if AT LEAST ONE input is 1.
| A | B | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
NOT Gate
Inverts the input.
| Input | Output |
|---|---|
| 0 | 1 |
| 1 | 0 |
XOR (Exclusive OR)
Output 1 if inputs are DIFFERENT.
| A | B | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Exam Summary
Logic gates are electronic circuits that implement Boolean logic by processing binary inputs to produce binary outputs, enabling decision making, data processing, and control in all digital systems.